Biopolímeros (4831)

Módulo 2. Ficha 2.3

FUERZAS QUE DETERMINAN LA ESTRUCTURA MACROMOLECULAR

2.3. Interacciones que implican la polarizabilidad de átomos y moléculas.

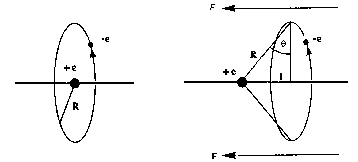
2.3.1. Interacción carga-dipolo inducido:

Si un átomo con sólo un electrón que gira con simetría esférica alrededor del núcleo (sistema sin momento dipolar permanente) es sometido a un campo eléctrico E, se produce una separación l de la órbita del electrón respecto de la que tenía cuando no había campo eléctrico presente. Como consecuencia aparece un momento dipolar inducido mind =l.e que es proporcional a la magnitud del campo aplicado. A la constante de proporcionalidad entre el campo aplicado y el momento dipolar inducido se le llama polarizabilidad a0.

 

mind =l.e =a0E                       [2.3.1.1]

[2.3.1.2]

Fint es la fuerza de atracción electrostática entre el núcleo y el electrón promediada al movimiento circular del electrón respecto al núcleo con un ángulo q entre el plano de la órbita y la dirección de R. La fuerza que ejerce el campo eléctrico externo sobre el electrón (Fext = eE) tiene que neutralizarse con la fuerza que el núcleo ejerce sobre el electrón en la dirección del campo Fint. El equilibrio se produce porque ambas fuerzas son iguales lo que implica que mind =4pe0R3E y por tanto a0 =4pe0R3
Las unidades de polarizabilidad son 4pe0 x (volumen), es decir C2 m2 J-1. A la polarizabilidad de átomos y moléculas que proviene de este desplazamiento de los electrones se le llama polarizabilidad electrónica. Por ejemplo para el agua a0/4pe0= 1'48.10-30 m3 = (0'114 nm)3, donde 0'114 es un 15% menor que el radio de la molécula de agua (0'135 nm). Al término a0/4pe0 se le llama volumen de polarizabilidad.

Polarizabilidadades de algunos enlaces y moléculas.
C - C  0'48 C = O 1'36 CH4 2'6
C = C 1'07 H2O 1'48 CCl4 10'5
O - H 0'73 H3N 2'3 C6H6 10'3
Las unidades de a0están en unidades de (4pe0) A3 = (4pe0) 10-30 m3

Aunque una molécula tenga momento dipolar permanente, en ausencia de campo y como resultado de la rotación libre molecular, el efecto promedio temporal de ese momento dipolar eléctrico es nulo (es como si la molécula no fuera dipolar). La presencia de un campo eléctrico externo deshace esta nulidad, ya que la interacción entre el campo y el dipolo, por débil que esta sea, implica la aparición de una dirección privilegiada de alineamiento de la molécula y por tanto una resultante neta del momento dipolar molecular en la dirección del campo eléctrico de mcosq. A temperaturas en las cuales la energía de interacción dipolo-campo (Em) sea del orden de la energía térmica (kT), la dirección en la que se orienta el dipolo no será única, sino que serán posibles un abanico de posibles direcciones de orientación cuya distribución de probabilidad puede representarse mediante una distribución de Boltzman. Es decir aparecerá una resultante neta del momento dipolar molecular en la dirección del campo cuyo valor promedio será:

<m>= <mcosq exp( mcosq E/kT)> = Em2<cos2q> /kT = Em2 /3kT

Es decir aparece una resultante neta del momento dipolar distinta de cero (Em2 /3kT ) como consecuencia de que la molécula sometida a la acción del campo eléctrico. Esta resultante neta del momento dipolar en las moléculas polares por efecto del campo externo se superpone a la polarizabilidad electrónica consecuencia de la distorsión de la nube electrónica molecular. Teniendo en cuenta la expresión del momento dipolar inducido (aE), en el valor total de este momento dipolar inducido, habrá una componente que no es electrónica, sino que está solo causada por la orientación. A este término, por tanto, se le llama por tanto polarizabilidad orientacional o de orientación. Por tanto para temperaturas en donde el producto del momento dipolar de estas moléculas por el campo aplicado sea mucho menor que kT puede considerarse que la polarizabilidad de este tipo de moléculas es: a =a0 + m2/3kT. Por ejemplo una molécula con un momento dipolar de 1 D a 300 K tiene una polarizabilidad de orientación de:

Valor que es del orden del de la polarizabilidad electrónica de la molécula. Cuando la temperatura es muy baja o los momentos dipolares moleculares muy grandes, los dipolos moleculares se alinean por completo con respecto al campo externo, con lo que el concepto de polarizabilidad por orientación desaparece.

¿Cuánto vale la energía de interacción entre un ión i el dipolo inducido por él en una molécula cercana (interacción ión-dipolo inducido)? Sea una molécula polarizada por un ión de carga Ze, situado a una distancia r de ella; el campo eléctrico que siente tiene una magnitud de E = Ze/ 4pee0r2, por lo tanto el momento dipolar inducido tendrá un valor de mind = a Ze/ 4pee0r2. La energía de interacción entre este ión y el dipolo inducido por él, Ui-ind, tiene un valor de - aE2/2 y es la mitad de lo que valdría si ese dipolo hubiera sido permanente. Este valor proviene de que a la energía de interacción entre el campo (E) y el dipolo (aE), cuyo valor sería -aE2, hay que restarle la energía necesaria para formar ese dipolo, el cual puede estimarse en (vease figura anterior):

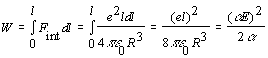[2.3.1.3]

Es decir que la energía de interacción entre el ión y el dipolo inducido es:  Ui-ind = - aE2 + W = - aE2/2  , tal como se habia apuntado anteriormente.

Si se sustituye el campo por su valor y la polarizabilidad por la suma de la polarizabilidad electrónica y la de orientación, si la molecula es polar, la expresión de la interacción entre el ión-dipolo inducido es:

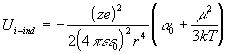[2.3.1.4]

 

2.3.2. Interacciones dipolo-dipolo inducido

De la misma forma que un ión puede inducir la formación de un dipolo en una molécula neutra, también un dipolo permanente puede inducir la formación de otro dipolo en moléculas neutras. La energía de interacción entre ambos dipolos (el permanente y el inducido) es:

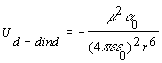[2.3.2.1]

En el caso más general en el que las dos moléculas tengan dipolos permanentes, m1ym2 con polarizabilidades a01 y a02, la energía de interacción entre ellas es:

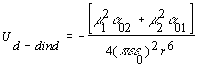[2.3.2.2]

Esta energía de interacción también se conoce con el nombre de interacción de Debye o interacción de inducción y es otra de las componentes de las llamadas interacciones de Van der Waals que estudiaremos en el siguiente apartado.

Ficha anterior Ficha Siquiente
Biopolímeros. J. Donoso.Página actualizada en Febrero 2006