 |
Biopolímeros (4831) |
 |
|
Módulo 2. Ficha
2.4
|
|
|
Biopolímeros (4831) |
|
|
Módulo 2. Ficha
2.4
|
FUERZAS QUE DETERMINAN LA ESTRUCTURA MACROMOLECULAR
2.4. Fuerzas de dispersión: Interacciones de Van der Waals
Las interacciones que se acaban de describir en los módulos 2.2 y 2.3 siempre tienen un origen electrostático, bien sea porque exista una carga o porque exista un dipolo que genere un campo eléctrico. Existe aún otro tipo de interacciones entre las moléculas, todas las moléculas, aunque éstas sean totalmente neutras, por ejemplo las que existen entre los átomos de helio o entre las moléculas de los hidrocarburos o del dióxido de carbono. Estas interacciones están causadas por las llamadas fuerzas de dispersión, fuerzas de London, fuerzas electrodinámicas, fuerzas de fluctuación de cargas o fuerzas dipolo inducido-dipolo inducido. Sus principales características son:
Las fuerzas de dispersión son de naturaleza cuántica y su tratamiento riguroso se hace con conceptos de electrodinámica cuántica. Una justificación cualitativa de las mismas podría hacerse con las siguientes consideraciones: para un átomo neutro, tal como el He o el H, la distribución de carga electrónica promediada en el tiempo proporciona un momento dipolar nulo. No obstante en un momento particular -en el átomo de H en cualquier momento particular- la posición relativa del núcleo y de los electrones hará que el momento dipolar no sea nulo. Este momento dipolar instantáneo genera sobre los átomos vecinos un momento dipolar inducido y en consecuencia se establece una interacción entre momento dipolar instantáneo y momento dipolar inducido. Este es el origen de las fuerzas de dispersión que existen entre todos los átomos y moléculas.
El tratamiento de London de este tipo de interacciones usando la teoría de perturbaciones de la mecánica cuántica indica que dependen del potencial de ionización de los átomos o las moléculas implicadas y de la inversa de la distancia entre ellos elevada a la sexta potencia.
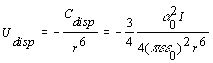[2.4.1]
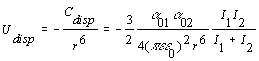[2.4.2]
La expresión [2.4.1] se refiere a interacciones de dispersión entre partículas idénticas en donde I es el potencial de ionización y a0 es la polarizabilidad y la expresión [2.4.2] es la interacción entre dos partículas distintas.
Estas fuerzas de dispersión de London de la misma forma que las ya descritas, interacciones de Keeson y las de Debye,dependen de 1/r6 y constituyen la tercera contribución al término atractivo de las interacciones de Van der Waals.
Estimación de la magnitud de las fuerzas de dispersión de London para dos átomos o dos moléculas pequeñas con a0 /4pe0 = 1'5 10-30 m3y I = 2 10-18J, valores típicos de estas magnitudes, a una distancia de contacto r=s =0'3 nm: Udisp(s)= -4'6 10-21 J. Valor que es aproximadamente igual a kT.
 |
| La figura muestra la curva teórica determinda para el valor de las fuerzas de dispersión de London entre átomos de argón en línea discontinua y la compara con la determinada experimetalmente. Figura tomada del libro de Israelachvili. |
Cuando los átomos o moléculas (en estados energéticos no favorables para la formación de enlaces químicos) empiezan a estar muy cerca y las nubes electrónicas respectivas empiezan a interaccionar aparecen las llamadas fuerzas repulsivas estéricas o repulsiones de intercambio. Estas fuerzas son de muy corto alcance y aumentan bruscamente a partir de una cierta distancia. Evidentemente estas fuerzas son de naturaleza cuántica y no se dipone de una ecuación general que permita describir estas interacciones. Existe un conjunto de potenciales empíricos que, dependiendo de los casos, se ajustan más o menos bien a los resultados experimentales que se pretende describir. Entre ellos están: (a) la función de potencial de esferas rígidas, (b) la función tipo inversa y (c) la función tipo exponencial.
(a) Potencial de esferas rígidas: U(r) = + (s/r)n ; n=¥
Si los átomos y moléculas se consideran como esferas rígidas, es decir incompresibles, las fuerzas repulsivas se hacen de pronto infinitas a una cierta separación (s). Este modelo tan simple refleja el hecho de que en muchos líquidos y sólidos las moléculas o los átomos se empaquetan y se comportan como si realmente fueran esferas rígidas o bolas de billar y mantienen un radio fijo característico de cada átomo o molécula. Se define así el diámetro de esferas rígidas o de empaquetamiento de Van der Waals (s). Este diámetro puede determinarse mediante medidas experimentales de difracción de rayos X o de neutrones o por medidas de viscosidad, de difusión, etc. Los radios de Van der Waals de los átomos y moléculas pequeñas están entre 0'1 y 0'2 nm. No hay que confundir este radio de Van der Waals con el radio covalente de un átomo que es la mitad de la distancia internuclear en la molécula diatómica. En general los radios covalentes de enlaces simples suelen ser 0'08 nm más cortos que los radios de Van der Waals de los átomos no enlazados.
(b) Potencial de función inversa: U(r) = + (s/r)n ; n es un número entre 9 y 16
(c) Potencial de función exponencial: U(r)= + ce-r/s0 ; donde c y s0 son dos parámetros ajustables.
Estos dos últimos potenciales son mucho más realistas que el de esferas rígidas y permiten tener en cuenta que tanto los átomos como las moléculas son sistemas deformables.
 |
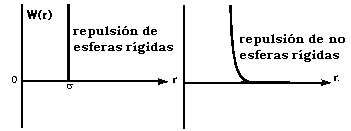| Forma de la función de potencial de esferas rígidas (a) (izquierda) y de potenciales que tienen en cuenta la deformación molecular (b) (c) (derecha) |
De acuerdo con los apartados anteriores, la función total que describa las interacciones entre dos moléculas i/o iones, debe contener un término de potenciales repulsivos, un término de interacciones de Van der Waals y los términos de interacciones electrostáticas fuertes. En el caso de moléculas no iónicas y poco polares es sufiente con una función de potencial de dos términos, uno atractivo y uno repulsivo.
Una de las funciones de potencial más usadas para la descripción de estas contribuciones atractivas y repulsivas es el llamado potencial de Lennard - Jones o potencial "6-12" que viene dado por la expresión:
U(r)= A/r12 - B/r6 = 4 Î [(s/r)12 - (s/r)6] [2.6.1]
El término B/r6 recoge todas las interacciones atractivas tipo interacciones de dispersión o de London, interacciones de inducción o de Debye e interacciones de orientación o de Keeson. El término A/r12 recoge las interacciones de tipo repulsivo con un potencial del tipo función inversa descrito en el apartado anterior. De esta descripción queda claro que en moléculas con fuertes interacciones electrostáticas, ión-ión, ión-dipolo o dipolo-dipolo, se han de añadir las funciones de los potenciales a los que dan lugar este tipo de interacciones y que en la fórmula [2.6.1] no están contempladas.
 |
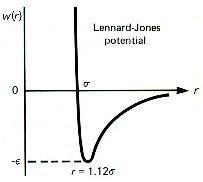| Función de potencial total de Lennard-Jones |
En este potencial de
Lennard - Jones hay que resaltar que en esta función el parámetro
s no es el diámetro
molecular, ya que U(r) se anula cuando r=s , y el mínimo
de la energía sucede cuando r= 21/6s = 1'12 s. En el mínimo, el
valor de la energía es, U(r) = - Î , siendo la contribución
de las fuerzas atractivas de Van der Waals -2Î y el de las fuerzas repulsivas
+Î .
| Radios de Van der Waals de algunos grupos atómicos (A) |
Energía de Van der Waals
de algunos pares de átomos a la separación de equilibrio
(kJ/mol)
|
||
|
-H
|
1,2
|
H...H
|
0'0778
|
| -O (hidroxilo) |
1,5
|
=O...O=
|
0'217
|
| =O (carbonilo) |
1,5
|
N....N
|
0'572
|
| - N (amida) |
1,55
|
C...C
|
0'284
|
| -NH3+ |
1,86
|
C...C*
|
1'891
|
| CH (trigonal) |
1,7
|
*carbono carbonílico o carboxílico
|
|
| S |
1,8
|
||
Ficha
anterior 
|
 Ficha
Siquiente |
 |