 |
Biopolímeros (4831) |
 |
|
Módulo 7. Ficha
7.2
|
 |
Biopolímeros (4831) |
 |
|
Módulo 7. Ficha
7.2
|
INTERACCIÓN BIOPOLÍMEROS-LIGANDOS

La figura anterior es una representación esquemática del modelo de una macromolécula con dos sitios de unión idénticos. Existen dos formas microscópicas de la molécula con un sitio ocupado y sólo una de la molécula con los dos sitios ocupados o con los dos sitios vacíos. Que los dos sitios de unión sean idénticos, no significa que tengan las mismas constantes de unión, sino que son indistinguibles y por tanto no hay ningún orden preestablecido sobre cual se llenará primero. Se tienen por tanto dos constantes de unión microscópicas definidas como:
;

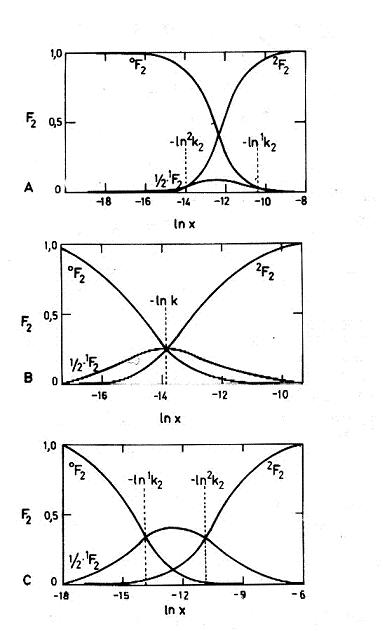
Variación relativa de las energías de Gibbs del sistema cuando se adicionan la primera y la segunda molécula de ligando: Cooperatividad
- Si X = 1/ 1k2 (ln X = - ln1k2 ); 0F2 = (1/2) 1F2
- Si X = 2k2 (ln X = - ln2k2 ) 2F2 = (1/2) 1F2
Teniendo en cuenta que 0M2 = 0M'2 ; 1M2 =2 1M'2 ; 2M2 = 2M'2 puede comprobarse que el polinomio de unión en este caso es: 2Px = 1 + 2 1k2 x + 1k2 2k2 x2; y la fracción molar de cada una de las formas es:
0F2 = 1/2Px ; 1F2 = 2 1k2 x / 2Px ; 2F2 = 1k2 2k2 x2 / 2Px
 Ficha
Siquiente Ficha
Siquiente |